Обучение задачам

Основные этапы обучения решению задач в начальных классах.



По способу восприятия действительности, всех людей можно разделить на три большие группы: визуалы, аудиалы, кинестетики. Если вы попросите обучающихся подумать о лете, то некоторые из них представят сочный цвет зелёной травы и яркие краски летних цветов. Это дети-визуалы, которые лучше воспринимают информацию с помощью зрения. Другие дети будут ассоциировать лето с весёлым детским смехом, шумом листвы и мелодией тёплого летнего дождя. Это дети-аудиалы, лучше воспринимающие информацию через слух. А остальная часть обучающихся вспомнит ощущение жгучего солнца и горячего песка. Это дети-кинестетики, которые лучше воспринимают мир на ощупь.

Согласно статистике, 60% обучающихся – это визуалы. Такие дети труднее воспринимают информацию на слух. Для лучшего усвоения материала им необходима наглядность - картинки, иллюстрации, презентации или специальные пособия. Важное место на уроках математики занимают текстовые задачи. Решая их, обучающиеся получают возможность применить полученные теоретические знания на практике. Но, к сожалению, многие дети, а именно, дети-визуалы, сталкиваются с большими трудностями в решении текстовых задач, так как они не сопровождаются иллюстрациями.

В третьем классе обучающиеся знакомятся с новым видом текстовых задач, в условии которых фигурируют различные предметы: карандаши, книги, апельсины или любые другие материалы. Величины этих предметов обозначаются числовыми значениями. Но дети-визуалы с трудом могут определить взаимосвязь между величинами и их числовыми значениями. Поэтому перед учителем стоит задача, организовать дополнительную работу, включающую в себя специальные игры и упражнения, которые помогут детям получить опыт обозначения числом разных предметов, их стоимость, цену, количество и другое.

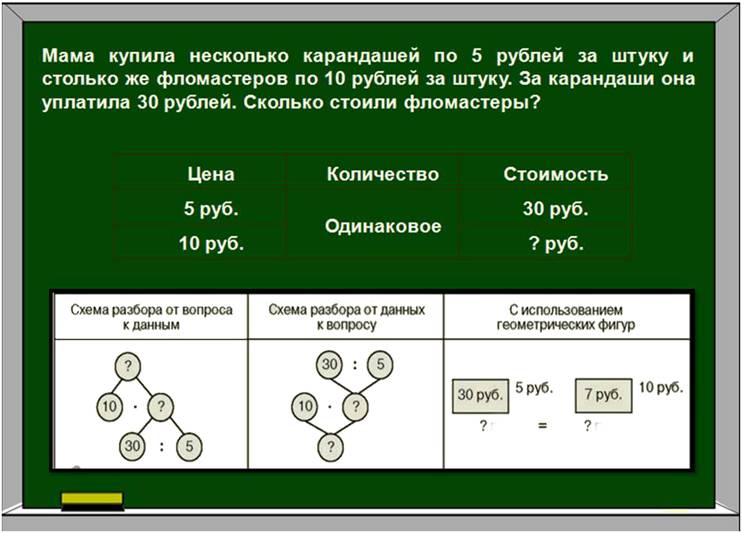
Авторы учебников по математике для начальной школы: Демидова Т.Е., Козлова С.А., Тонких А.П. (УМК «Школа 2100»), Истомина Н.Б. (УМК «Гармония»), Рудницкая В.Н. (УМК «Начальная школа XXI века») и другие, предлагают задачи, в которых прослеживается зависимость между величинами. Большинство из них направлены на поиск ответов в области скорости-времени-расстояния и цены-количества-стоимости.

Как показал опыт работы с такими задачами, обучающиеся сталкиваются с небольшими трудностями. Поэтому перед учителем стоит непростая задача – планомерно, шаг за шагом, начиная с первого класса, знакомить детей со структурой текстовых задач, с особенностями решения задач различных видов, а также помогать обучающимся находить верный путь в решении той или иной задачи путём составления краткой записи и подробного плана решения.



Перед тем, как приступить к основным этапам решения текстовой задачи, необходимо провести тщательную подготовительную работу. Именно от подготовительного этапа зависит дальнейшее понимание особенностей задач на нахождение четвёртого пропорционального. Самое главное на этом этапе, чтобы обучающиеся увидели взаимосвязь величин между собой. В этом могут помочь различные игровые ситуации, наглядные пособия или красочные презентации. Когда обучающиеся успешно преодолеют подготовительный этап, можно приступить к основному этапу решения текстовых задач на простое тройное правило.

Основной этап мы рассмотрим на примере одной из задач: «Ученик купил несколько карандашей по 4 руб. за штуку и столько же фломастеров по 8 руб. за штуку. За карандаши он заплатил 20 руб. Сколько стоили фломастеры?».

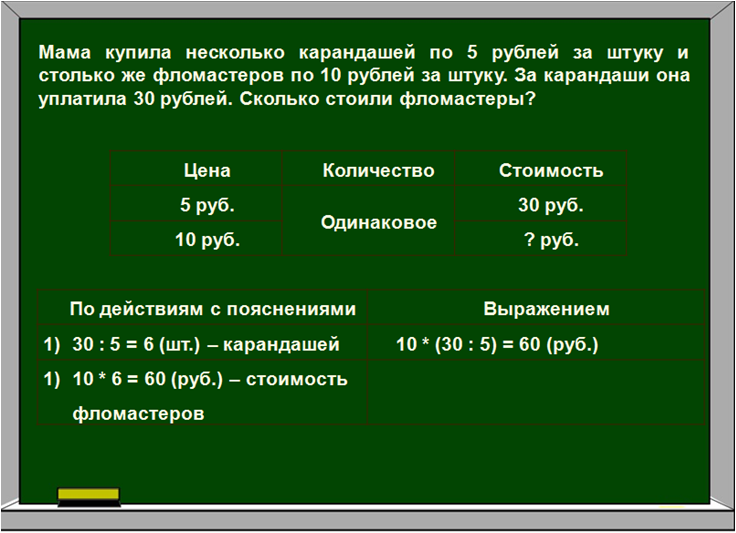
Анализ условия задачи:

Учитель: О чём говорится в задаче?

Ученики: О карандашах и фломастерах.

Учитель: Что обозначает число 4?

Ученики: Число 4 – цена одного карандаша.

Учитель: А что обозначает число 8?

Ученики: Число 8 – это цена одного фломастера.

Учитель: Что известно о стоимости карандашей?

Ученики: Стоимость карандашей – 20 рублей.

Учитель: Что спрашивается в задаче?

Ученики: Сколько денег заплатили за фломастеры?

Планирование решения задачи:

Учитель: Можем ли мы сразу ответить на вопрос задачи?

Ученики: Нет.

Учитель: Почему?

Ученики: Нам неизвестно, сколько купили фломастеров.

Учитель: Можем ли мы узнать, сколько купили фломастеров?

Ученики: Да.

Учитель: Как мы узнаем?

Ученики: Так как карандашей и фломастеров купили одинаковое количество, то мы можем узнать, сколько купили карандашей (а значит, что и фломастеров столько же).

Учитель: Какое арифметическое действие мы будем использовать?

Ученики: Деление.

Учитель: Как это запишем?

Ученики: 20:4=5 шт.

Учитель: Зная, сколько купили карандашей, можем ли мы узнать, сколько купили фломастеров?

Ученики: Да.

Учитель: Почему?

Ученики: Потому что мы знаем, что фломастеров и карандашей было одинаковое количество.

Учитель: Какое арифметическое действие мы будем использовать?

Ученики: Умножение.

Учитель: Как запишем?

Ученики: 8х5=40 руб.

Учитель: Мы ответили на вопрос задачи?

Ученики: Да.

Учитель: Так сколько денег заплатили за фломастеры?

Ученики: 40 рублей.

Выполнение плана решения задачи

Проверка решения задачи

Способ I - решение задачи другим способом:

Во сколько раз больше стоит фломастер, чем карандаш?
8 : 4 = 2 руб.
Сколько заплатили за карандаши?
40 : 2 = 20 руб.

Способ II - составление и решение обратной задачи:


4 х (40 : 8) = 20 руб.
Вывод: задача решена верно.

Составление ответа на вопрос задачи

Ответ: 40 рублей стоили фломастеры.

Анализ решений задачи

Этот этап необходим для того, чтобы обсудить с обучающимися, какой из найденных способов решения задачи более удобный и рациональный. Если грамотно организовать подготовительный этап и чётко следовать плану основного этапа, у обучающихся не возникнут трудности в решении задач на простое тройное правило. Самое главное, чтобы дети научились видеть взаимосвязь между числовыми значениями различных величин. Именно это является ключевым моментом в задачах данного вида.

Марина Фурзикова
учитель нач. классов
МБОУ «Гимназия № 14
г. Йошкар-Олы», Респ. Марий-Эл